LUMIÈRE - Réflexion et réfraction

LUMIÈRE - Réflexion et réfraction

Un rayon lumineux se propageant dans un milieu matériel (ou dans le vide) est généralement dévié lorsqu’il en rencontre un autre par diffusion, ou bien par réflexion ou par réfraction, selon qu’il reste ou non dans le premier milieu. Ces changements de direction obéissent aux lois de l’optique géométrique (Snell-Descartes, cf. OPTIQUE). On montrera comment ces lois se déduisent d’un principe énoncé en 1658 par le Français Fermat, et l’on indiquera ensuite comment l’énergie lumineuse se partage entre les faisceaux réfléchis et transmis. On donnera enfin quelques détails sur diverses réalisations faisant intervenir ces phénomènes.

1. Déviations d’un rayon lumineux

Propagation, indices, chemin optique

Les faisceaux lumineux peuvent être (sous certaines réserves indiquées à l’article DIFFUSION DE LA LUMIÈRE - Météorologie) considérés comme formés de rayons, le long desquels une énergie vibratoire se propage par ondes.

Dans un milieu matériel homogène, la propagation est rectiligne, la vitesse v étant inférieure à sa valeur c dans le vide, qui est voisine de 300 000 km/s; v varie avec la fréquence 益 = 1/T de la radiation considérée, donc aussi avec sa longueur d’onde dans le vide = c T. Le rapport n = c /v est l’indice de réfraction du milieu pour cette radiation.

Dans un milieu non homogène, n varie en général d’un point à un autre et les rayons lumineux peuvent être courbes; dans un milieu non isotrope, n est fonction de la direction de propagation.

Soit A et B deux points d’un même rayon rectiligne ou non (fig. 1) et soit ds un élément infiniment petit de cette trajectoire lumineuse. On appelle chemin optique de A à B, représenté par L ou encore par [AB], l’intégrale:

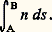Comme l’élément ds est parcouru en un temps:

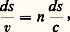le chemin optique est l’espace ct que parcourait la lumière dans le vide pendant le temps:

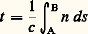qu’elle met en réalité pour aller de A à B. On peut aussi, comme on va le voir, calculer L par l’expression donnée ci-dessus sur des trajectoires qui ne sont pas nécessairement celles de la lumière.

Principe de Fermat

Le principe de Fermat peut s’énoncer ainsi: Toute trajectoire T effectivement suivie par une radiation correspond à un chemin optique L = AB «stationnaire», c’est-àdire minimal ou maximal par rapport au chemin optique L + d L = A B sur une trajectoire T , infiniment voisine de T, et joignant les mêmes points; on peut donc poser d L = 0.

On n’étudiera ci-après que le cas de milieux homogènes, dans lesquels à un chemin géométrique s correspond un chemin optique ns . Soit (fig. 2) ぴ le vecteur unitaire porté par le rayon AB, soit d Aet d Bles déplacements infiniment petits AA et BB ; alors d L est égal au produit scalaire nu[d B漣 d A 轢].

Soit maintenant un rayon lumineux AIB (fig. 3) qui traverse en I la surface, appelée dioptre , séparant deux milieux d’indices n ¹ et n ²; ぴ¹ et ぴ² étant les vecteurs unitaires sur AI et IB, la variation du chemin optique quand on passe du rayon AIB au parcours infiniment voisin AI B, qui traverse le dioptre en I tel que 轢II = d I 轢, est:

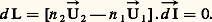Les deux vecteurs n ² ぴ² 漣 n ¹ ぴ¹ et d Isont donc orthogonaux. Puisque 轢II est tangent au dioptre, on peut donc poser:

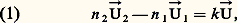ぴ étant le vecteur unitaire sur la normale ¹I² au dioptre et k ayant une valeur convenable; ぴ¹, ぴ² et ぴ sont par suite dans un même plan, ce qui constitue la première loi de Descartes pour la réfraction: le rayon réfracté IB se trouve dans le plan d’incidence AIN.

Soit i ¹ et i ² les angles que font respectivement AI et IB avec I¹ et I². En multipliant scalairement les deux membres de la relation (1) par un vecteur unitaire porté par 轢II , on est conduit à:

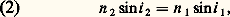ce qui est la deuxième loi de Descartes pour la réfraction.

Les lois relatives à la réflexion se résument ainsi: Le rayon réfléchi IC est symétrique du rayon incident AI par rapport à la normale I¹. Elles s’établissent par un raisonnement analogue au précédent. Il est parfois commode de faire apparaître l’angle de réflexion:

à la place de i ² dans des relations telles que la formule (2) en y remplaçant n ² par 漣 n ¹.

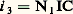Toute l’optique géométrique se déduit des lois de Descartes qui viennent d’être établies à partir de l’énoncé de Fermat; on peut aussi considérer ce dernier non plus comme un principe mais comme un théorème, démontré comme conséquence des lois de la réflexion et de la réfraction; ces lois sont alors admises comme résultats d’expérience.

Indices absolus et relatifs

On rappellera ci-après les méthodes utilisées pour la mesure des indices. Les indices des gaz, très voisins de l’unité, varient, pour une même radiation, en fonction de la température et de la pression, comme l’indique la loi de Gladstone:

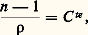福 étant la masse volumique. Les indices des liquides ou des solides ne sont qu’exceptionnellement inférieurs à 1,3 ou supérieurs à 2. Pour les substances usuelles, ils diminuent régulièrement quand la radiation utilisée passe de l’extrémité violette à l’extrémité rouge du spectre (cf. LUMIÈRE – Dispersion et absorption). Le tableau 1 l’indique dans quelques cas.

La formule (2) peut s’écrire:

en posant i ¹ = i (angle d’indicence), i ² = r (angle de réfraction) et n ²/n ¹ = n . Le rapport n ainsi défini est appelé indice relatif du milieu 2 par rapport au milieu 1, n ¹ et n ² étant les indices absolus (ou indices par rapport au vide) de ces deux milieux. L’indice absolu de l’air, dans les conditions normales de température et de pression, est, pour toutes les radiations visibles, voisin de 1,000 3, ce qui permet de confondre, en première approximation, l’indice absolu d’un liquide ou d’un solide quelconque avec son indice relatif par rapport à l’air.

Angle limite

La formule (2) montre que, si n ² 礪 n ¹, tout rayon incident pénètre dans le second milieu (supposé transparent) en se rapprochant de la normale (fig. 4 a). Pour la valeur maximale 神/2 de i ¹, i ² atteint une valeur maximale l telle que sin l = 1/n ²; on appelle cette valeur maximale l angle limite de réfraction . Pour n = 4/3, l = 48,6⁰; pour n = 3/2, l = 41,7⁰. Si n ² 麗 n ¹, le rayon réfracté est plus écarté de la normale que le rayon incident (fig. 4 b). Dès que i ¹ est supérieur à l’angle limite l , le rayon réfracté n’existe plus (on ne peut en effet avoir sin i ² 礪 1); l’énergie incidente se retrouve alors entièrement dans le rayon réfléchi, et l’on dit qu’il y a réflexion totale .

2. Réflexion et réfraction de l’énergie lumineuse

Sauf dans le dernier cas considéré ci-dessus, un flux lumineux incident F^{i [cf. PHOTOMÉTRIE]} se trouve divisé en un flux réfléchi F^r , en un flux transmis F^t et en un flux absorbé F^a . On appelle facteur de réflexion et facteur de transmission les rapports R = F^r /Fⁱ et T = F^t /Fⁱ . Lorsque F^a est négligeable, on a, en vertu du principe de conservation de l’énergie, R + T 力 1.

Cas de la réflexion «vitreuse»

Le cas de la réflexion vitreuse a été étudié par Fresnel, considérant que le second milieu est, comme le premier, un diélectrique ou le vide. Le facteur de réflexion dépend des valeurs des indices n ¹ et n ² , de l’angle d’incidence i et de l’état de polarisation de la lumière (cf. LUMIÈRE - Polarisation). Soit R size=1^瑩 sa valeur pour une lumière polarisée rectilignement et vibrant dans le plan d’indice et R size=1^旅 sa valeur pour une vibration perpendiculaire; pour une lumière naturelle, R = (R size=1^瑩 + R size=1^旅)/2. Les variations de R size=1^瑩, de R size=1^旅 et de R ont une allure représentée sur la figure 5 a pour n ¹ 麗 n ² et sur la figure 5 b dans le cas contraire. On notera que R size=1^瑩 passe par un minimum nul pour une certaine valeur de i (incidence brewstérienne égale à 55⁰ environ pour le verre ordinaire).

Au voisinage de l’incidence normale, les trois facteurs ont une valeur commune:5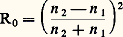

qui devient:

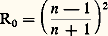pour une substance d’indice n baignée dans l’air.

Le tableau 2 donne les valeurs de R et de T pour n ¹ = 1 et n ² = 1,5.

Réflexion «métallique»

Les métaux polis ont un facteur de réflexion élevé dès l’incidence normale. En lumière polarisée, les courbes donnant R size=1^瑩 et R size=1^旅 en fonction de l’incidence i ont l’allure qu’indique la figure 5 c.

Le facteur de réflexion des métaux varie beaucoup avec la longueur d’onde. Pour l’argent, par exemple, sa valeur sous l’incidence normale, de l’ordre de 0,92 dans le visible et supérieur à 0,95 dans l’infrarouge, tombe à moins de 0,1 dans l’ultraviolet.

Couches minces

On peut modifier le facteur de réflexion d’une surface S polie en la recouvrant de une ou de plusieurs couches minces métalliques ou diélectriques: le plus souvent, le matériau est vaporisé dans le vide et vient se condenser sur S.

Une couche d’indice n et d’épaisseur e telle que ne =/4 annule le facteur de réflexion pour la longueur d’onde lorsque n = N, N étant l’indice de la substance sur laquelle cette couche est déposée. On ne dispose généralement pas de matières pouvant satisfaire à cette dernière condition, mais on sait réaliser des couches antireflets améliorant la transparence et surtout réduisant brutalement la lumière parasite dans les instruments qui comportent de nombreuses surfaces de séparation air-verre (cf. INTERFÉRENCES LUMINEUSES et OPTIQUE - Images optiques).

Inversement, on peut obtenir des miroirs à haut facteur de réflexion en les recouvrant de couches diélectriques multiples, d’épaisseurs convenables et d’indices alternativement faibles et forts: on a atteint 0,996 pour certains miroirs de laser. Le domaine de longueurs d’onde bien réfléchies peut, selon la nature des couches, être relativement étroit ou s’étendre à tout le spectre visible (fig. 6).

On sait aussi réaliser des miroirs semi-transparents , appelés «lames séparatrices», permettant de diviser un faisceau incident en deux autres (réfléchi et réfracté), dont les énergies sont dans un rapport déterminé (égales, par exemple). Il y a deux types de telles lames, les unes à couche mince métallique, dont les propriétés optiques sont à peu près uniformes dans un assez large domaine spectral, mais qui sont notablement absorbantes, les autres à couches diélectriques multiples, qui n’absorbent presque pas, mais dont les facteurs R et T ne sont à peu près constants que dans un domaine spectral étroit.

3. Applications

On se reportera, en ce qui concerne la «taille» des surfaces de miroirs, de prismes ou de lentilles, à l’article VERRE.

Miroirs

Les miroirs usuels sont en métal ou, plus souvent, en verre recouvert sur sa face arrière d’une couche d’étain amalgamé, ou mieux d’argent, ou encore d’aluminium; la réflexion sur la face avant du verre donne alors une seconde image, relativement peu intense, mais pourtant inacceptable dans certains cas. Les miroirs d’optique sont donc métallisés sur leur face avant (en général, par dépôt d’aluminium vaporisé dans le vide). Leur forme (plane ou sphérique, par exemple) et leur polissage sont assurés avec des tolérances très strictes, de l’ordre de/10 (soit 0,05 猪m) pour des miroirs astronomiques. Pour des rayons peu écartés de l’axe (approximation de Gauss), la position et la grandeur de l’image A B d’une petite droite normale à l’axe formée par un miroir sphérique , de sommet S et de centre C (fig. 7), sont données par les relations algébriques:

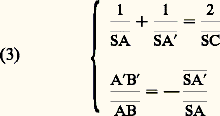En prenant comme sens positif celui de la lumière incidente, SC est négatif pour un miroir concave (cas de la figure 7), positif pour un miroir convexe .

Quand les déformations résultant des variations de température risquent d’altérer les images, on a recours à des matières dont le coefficient de dilatation 見 est très inférieur à celui du verre (pour lequel 見 力 10^-5), telles que la silice fondue ( 見 = 5,5 練10^-7), la silice dopée au titane ( 見 諒 0,3.10^-7) ou certaines céramiques vitrifiées. Les très grandes pièces peuvent être constituées par une mosaïque d’éléments hexagonaux soudés. Celles qui sont destinées aux satellites et aux fusées doivent être allégées, tout en gardant leur rigidité: on leur donne une structure nervurée.

Lentilles optiques

Les lentilles optiques sont des pièces transparentes, limitées par deux dioptres généralement sphériques (l’un d’eux pouvant être plan), exceptionnellement asphériques de révolution, cylindriques, toriques..., placées dans l’air, parfois accolées. Leurs indices, leurs dispersions, leurs formes, leurs positions relatives conditionnent la formation des images qu’elles sont destinées à fournir (cf. OPTIQUE - Images optiques, Optique instrumentale).

Pour une lentille mince de foyer image F et dont les deux faces sphériques ont des sommets voisins de S (ce foyer est le point où la lentille fait converger un faisceau de rayons parallèles à son axe), l’image A B d’une petite droite AB est, dans les conditions de l’approximation de Gauss, telle que:

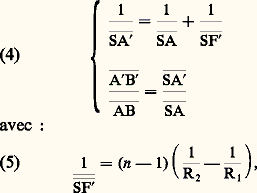R¹ et R² étant les rayons de courbure des deux faces de la lentille et n son indice par rapport à l’air où elle est supposée baigner.

La figure 8 illustre les divers cas possibles, selon la position de l’objet par rapport à S, pour une lentille convergente (SF positif, dans le sens de propagation de la lumière) ou divergente (SF négatif).

Les matériaux utilisés (tabl. 3) sont soit des verres minéraux très homogènes, soigneusement recuits (il en existe un très grand choix), soit des verres organiques , soit encore des cristaux ou des métaux convenant dans des domaines spectraux où le verre est peu transparent (cf. INFRAROUGE et ULTRAVIOLET).

Prismes réfringents

Un prisme optique est une pièce transparente qui est solide (ou contenue dans une enveloppe solide) et dont la surface comporte au moins deux dioptres plans qu’on appelle ses faces ; l’angle du dièdre qu’ils constituent est dit angle du prisme, l’intersection des faces étant son arête .

Soit un rayon incident SI pénétrant dans un prisme d’angle A et d’indice n par rapport au milieu qui l’entoure (généralement l’air, parfois le vide). Nous supposerons ce rayon situé dans un plan de section principale (perpendiculaire à l’arête). Il lui correspond un rayon réfracté II et, s’il n’y a pas réflexion totale en I , un rayon émergent IR , qui fait avec SI un angle de déviation D. Soit i , r , r , i les angles avec les normales en I et en I (comptés positivement dans le cas de la figure 9 a et négativement de l’autre côté des normales). Ils satisfont aux relations:

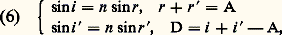qui se ramènent, lorsque i et A sont très petits, à:

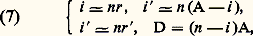où n est supérieur à 1; tout rayon incident pénètre dans le prisme, mais il n’émerge en I que si r est inférieur à l’angle limite l (fig. 9 b). La déviation D est une fonction croissante de A (si n et i sont constants) et de n (si i et A sont constants). Pour des valeurs données de n et de A, D varie en fonction de i comme l’indique la figure 10. Elle passe par un minimum D^m quand le cheminement des rayons est symétrique par rapport au plan bissecteur du prisme (fig. 9 c); n , A et D^m sont liés par la relation:

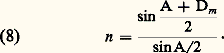Les spectrographes , servant à déterminer la composition spectrale d’une lumière, comportent souvent un ou plusieurs prismes. Sous la forme simple que schématise la figure 11, la lumière étudiée éclaire une fente S placée dans le plan focal d’une lentille ¹. À chaque point de S correspond un faisceau parallèle qui est dévié par le prisme P, et cela d’autant plus que sa longueur d’onde est plus courte. Les faisceaux reçus par la seconde lentille ² convergent dans son plan focal sur des images monochromatiques S de S qui peuvent s’échelonner entre le rouge (S ^r ) et le bleu (S ^b ), ou, au-delà de ces couleurs, former, selon le cas, un spectre de raies ou un spectre continu. Si l’on isole une de ces images par une «fente de sortie», l’instrument devient un monochromateur .

Prismes à réflexion totale

Les prismes à réflexion totale sont des combinaisons de deux dioptres plans et de un ou de plusieurs plans réfléchissants; il n’y a pas lieu de métalliser ceux-ci quand l’angle d’incidence est supérieur à l’angle limite. C’est le cas pour un prisme rectangle isocèle , utilisé comme l’indique la figure 12 a (noter que l’image A B de AB n’est pas symétrique de l’objet par rapport au miroir M, mais déviée à la traversée du prisme, comme elle le serait par la lame à faces parallèles dessinée en traits interrompus). Si la réflexion a lieu successivement sur les deux faces de l’angle droit (fig. 12 b), l’image A B est renversée par rapport à AB: ce dispositif et d’autres équivalents servent au redressement de l’image dans les jumelles à prismes.

Un prisme pentagonal , dont les faces réfléchissantes M¹ et M² font un angle de 45⁰ (fig. 12 c) ou de 135⁰, est tel que les rayons émergents sont normaux aux rayons incidents. Un trièdre trirectangle , à trois réflexions sur les faces de l’angle droit, impose à la lumière une déviation 神, la face de sortie, confondue avec la face d’entrée, compensant la déviation de cette dernière: on réalise ainsi un cataphote renvoyant la lumière vers sa source, quelle que soit l’orientation du prisme entre certaines limites.

Guides de lumière

Les guides de lumière sont des tiges transparentes recevant la lumière à l’une de leurs extrémités et la transmettant intégralement à l’autre (aux pertes par absorption près) après un nombre plus ou moins grand de réflexions totales. Ils peuvent être formés d’un faisceau de fibres très fines, dites fibres optiques en verre de fort indice, entourées d’une gaine d’indice faible. Cet ensemble n’est pas nécessairement rectiligne et peut être déformable. On utilise ces fibres dans certains dispositifs d’éclairage ou encore pour des transports point par point d’images dont la «définition» est conditionnée par le diamètre des fibres (de 5 à 100 猪m).

Les endoscopes destinés à l’examen de l’intérieur de cavités, en médecine ou dans l’industrie, comportent un guide de lumière formé par un mince barreau, généralement en silice, permettant d’éclairer la région à observer (fig. 13). Dans les fontaines lumineuses , un faisceau de lumière est dirigé à l’intérieur des veines liquides dont il rencontre les parois tantôt sous grande incidence, ce qui permet sa propagation par réflexion totale, tantôt sous une incidence inférieure à l’angle limite, la réfraction rendant alors le jet d’eau visible.

Réfractométrie

La mesure des indices de réfraction par la méthode du minimum de déviation utilise un montage rappelant celui de la figure 11, mais où le collimateur (système S¹), le prisme P et une lunette d’observation (ensemble de O² et d’un oculaire à réticule servant à observer son plan focal) sont orientables à volonté et portés par un goniomètre à cercle divisé, à l’aide duquel on peut mesurer les angles A et D^m intervenant dans la formule (8). Le prisme est constitué par la matière à étudier, si elle est solide; si elle est liquide, elle est contenue dans un prisme creux à faces transparentes et parallèles. L’angle A est le plus souvent voisin de 60⁰. Si la température, dont les variations influent notablement sur n , est assez uniforme et constante, l’indice peut être évalué (sur un très bon goniomètre) avec cinq décimales exactes pour un solide et quatre pour un liquide. Il existe d’autres méthodes de déviation permettant parfois des mesures plus rapides. La figure 14 représente un goniomètre automatique utilisable dans un large domaine de longueurs d’onde (de 0,25 à 20 猪m).

La figure 15 présente un exemple de réfractomètre faisant intervenir l’angle limite. L’échantillon E dont on veut mesurer l’indice n est posé sur un prisme auxiliaire solide P d’indice n ⁰ 礪 n . S’il n’y a pas de couche d’air interposée (lorsque l’échantillon est solide, on glisse à cet effet entre E et P une goutte de liquide d’indice supérieur à n ), les rayons rasants, tels que SI, pénètrent à travers la surface de séparation en faisant avec la normale l’angle limite l , tel que sin l = n /n ⁰. La face d’entrée dans E doit être normale à pour que ces rayons rasants existent: dans le plan focal objectif d’une lunette (non représentée) qui reçoit les rayons, tels que JL sortant de P, on observe une limite nette entre une plage claire et une plage obscure. Un cercle gradué permet d’évaluer l’angle d’émergence 見 dont on peut déduire n si l’on connaît n ⁰ et l’angle que font entre elles les faces d’entrée et de sortie de P.

Les indices de gaz sont trop voisins de l’unité pour qu’on puisse les mesurer avec précision par les méthodes précédentes: on les détermine (de même que les faibles variations d’indices des solides ou des liquides) par les méthodes interférométriques décrites à la fin de l’article MESURE - Mesures optiques.

Encyclopédie Universelle. 2012.